Wandai Blog 共被围观 1,801,436 次

在编写绘制、编辑导线功能的时候, 为了使得用户能够选取导线, 需要判断点到线段的距离是否在一个合适的范围内。

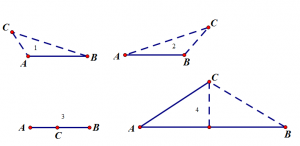
如图所示, 点与线短的关系有这么四种。

1、2、3都很好处理, 就是4。

这里, 可以使用向量的方式, 先求出∠A的余弦值cosA, 然后计算∠A的正弦值sinA, 最后AC*sinA为所求。

注意 $$\sin^2A =1-\cos^2A$$

而 $$\cos^2A = ( \frac{ \overrightarrow{AC} \cdot \overrightarrow{AB} }{ | \overrightarrow{AC} | \dot | \overrightarrow{AB} | } )^2 = \frac{ ( \overrightarrow{AC} \cdot \overrightarrow{AB} )^2 }{ | \overrightarrow{AC} |^2 \dot | \overrightarrow{AB} |^2}$$

由于我可以直接判断距离平方的数值, 于是就根本不需要根号了。

代码如下, 代码中的p, 为C点:

Public Class MyMath

    Public Shared Function Distance2(p As Point) As Integer
        Return p.X * p.X + p.Y * p.Y
    End Function

    Public Shared Function Distance2(a As Point, b As Point) As Integer
        Dim delta = a - b
        Return delta.X * delta.X + delta.Y * delta.Y
    End Function

    ''' <summary>
    ''' 点到线段的距离的平方
    ''' </summary>
    ''' <param name="a">线段一个端点</param>
    ''' <param name="b">线段一个端点</param>
    ''' <param name="p">待测点</param>
    ''' <returns>距离的平方</returns>
    ''' <remarks></remarks>
    Public Shared Function PointToLine2(a As Point, b As Point, p As Point) As Double
        Dim AP = p - a
        Dim d2AP = Distance2(AP)
        If d2AP = 0 Then
            Return 0.0
        End If

        Dim BP = p - b
        Dim d2BP = Distance2(BP)
        If d2BP = 0 Then
            Return 0.0
        End If

        Dim AB = b - a
        Dim d2AB = Distance2(AB)
        If d2AB = 0 Then '3
            Return d2AP
        End If

        If d2BP > d2AB + d2AP Then '1
            Return d2AP
        End If

        If d2AP > d2AB + d2BP Then '2
            Return d2BP
        End If

        Dim APdotAB As Double = AP.X * AB.X + AP.Y * AB.Y

        Return d2AP - (APdotAB * APdotAB) / d2AB
    End Function

    ''' <summary>
    ''' 点到线段的距离
    ''' </summary>
    ''' <param name="a">线段一个端点</param>
    ''' <param name="b">线段一个端点</param>
    ''' <param name="p">待测点</param>
    ''' <returns>距离</returns>
    ''' <remarks></remarks>
    Public Shared Function PointToLine(a As Point, b As Point, p As Point) As Double
        Return Math.Sqrt(PointToLine2(a, b, p))
    End Function

    Public Shared Function PointToLine_way2(a As Point, b As Point, p As Point) As Double
        Dim AP = p - a
        Dim d2AP = Distance2(AP)
        If d2AP = 0 Then
            Return 0.0
        End If

        Dim BP = p - b
        Dim d2BP = Distance2(BP)
        If d2BP = 0 Then
            Return 0.0
        End If

        Dim AB = b - a
        Dim d2AB = Distance2(AB)
        If d2AB = 0 Then '3
            Return Math.Sqrt(d2AP)
        End If

        If d2BP > d2AB + d2AP Then '1
            Return Math.Sqrt(d2AP)
        End If

        If d2AP > d2AB + d2BP Then '2
            Return Math.Sqrt(d2BP)
        End If

        Dim x = Math.Sqrt(d2AP), y = Math.Sqrt(d2BP), z = Math.Sqrt(d2AB)
        Dim l = (x + y + z) / 2
        Dim s = Math.Sqrt(l * (l - x) * (l - y) * (l - z))
        Return 2 * s / z
    End Function

    Public Shared Sub test()
        Dim a As New Point(4, 2)
        Dim b As New Point(2, 4)
        Dim c As New Point(3, 4)

        Dim ans As Double

        Dim sw As New Stopwatch()

        Dim count = 10000000

        sw.Reset()
        sw.Start()
        For i = 1 To count
            ans = PointToLine(a, b, c)
        Next
        sw.Stop()
        Debug.Print(ans)
        Debug.Print(sw.ElapsedMilliseconds.ToString() + "ms")

        sw.Reset()
        sw.Start()
        For i = 1 To count
            ans = PointToLine_way2(a, b, c)
        Next
        sw.Stop()
        Debug.Print(ans)
        Debug.Print(sw.ElapsedMilliseconds.ToString() + "ms")
    End Sub

End Class

way2为参考文献(http://blog.csdn.net/yjukh/article/details/5213577)的方法, 还求了个面积, 然后求高, 十分奇妙。里面需要多次开方, 我认为性能损失很大。经过简单的测试, 性能似乎确实没有我的好, 除了1、2、3三种情况(然而这三种情况的代码是一样的啊喂 (((摔>_< )。

听说还有一种非常好的矢量算法, 不会。