今天物理课, 讲完全弹性碰撞模型。
物理课接近尾声的时候, 老师出了这样一道例题:
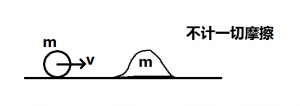
水平地面上, 有一座光滑的小山, 质量m, 小山不固定, 与地面无摩擦。
今令一初速为v的小球, 质量也为m, 从山的左侧撞山, 求最终小球以及山的速度。
首先, 我们需要考虑两种情况, 一是球无法越过小山, 二是球可以成功越过小山。
设小球的新速度为v1, 小山新速度为v2
首先, 分析第一种情况, 它可以等效为弹性碰撞, 列动量守恒式以及动能守恒式如下。
$$m\mathbf{v}=m\mathbf{v_1}+m\mathbf{v_2} (1)$$
$$\frac{1}{2}m\mathbf{v}^2=\frac{1}{2}m\mathbf{v_1}^2+\frac{1}{2}m\mathbf{v_2}^2 (2)$$
这个方程十分好解, 我们来解决它。
观察, 显然v1=v, v2=0是一组解。
下面来解另一组, 也就是v1≠v。
(1), (2)分别化简。
$$\mathbf{v}=\mathbf{v_1}+\mathbf{v_2} (3)$$
$$\mathbf{v}^2=\mathbf{v_1}^2+\mathbf{v_2}^2 (4)$$
移项得
$$\mathbf{v}-\mathbf{v_1}=\mathbf{v_2} (5)$$
$$\mathbf{v}^2-\mathbf{v_1}^2=\mathbf{v_2}^2 (6)$$
(6)分解因式得
$$(\mathbf{v}+\mathbf{v_1})(\mathbf{v}-\mathbf{v_1})=\mathbf{v_2}^2 (7)$$
由于v1≠v, (7)除以(5)得
$$\mathbf{v}+\mathbf{v_1}=\mathbf{v_2} (8)$$
代入(3)解得v1=0, v2=v。
这个解方程的方法也适用于解决普适的弹性碰撞方程, 是沈老师在讲解弹性碰撞时教给我们的, 十分好用。
由于球没有越过山, v1<v2, 第二组解是合理的。
v1=0, v2=v, 说明他们交换了速度、动能。
也就是球把所有能量给了山, 球自己什么也没留下。
接下来, 分析过山成功的情况, 由于球越过山, v1>v2, 第一组解是合理的。
v1=v, v2=0, 说明山最终什么能量也没有得到, 球保持原状。
我们的人生中也有许许多多类似的「山」, 根据如上分析, 越不过, 前功尽弃, 越过了才算成功。
(公式使用LaTeX撰写)
\documentclass{article}
\usepackage{ctex}
\author{twd2}
\title{hello, world}
\begin{document}
\maketitle
\begin{equation}
m\mathbf{v}=m\mathbf{v_1}+m\mathbf{v_2}
\end{equation}
\begin{equation}
\frac{1}{2}m\mathbf{v}^2=\frac{1}{2}m\mathbf{v_1}^2+\frac{1}{2}m\mathbf{v_2}^2
\end{equation}
\begin{equation}
\mathbf{v}=\mathbf{v_1}+\mathbf{v_2}
\end{equation}
\begin{equation}
\mathbf{v}^2=\mathbf{v_1}^2+\mathbf{v_2}^2
\end{equation}
\begin{equation}
\mathbf{v}-\mathbf{v_1}=\mathbf{v_2}
\end{equation}
\begin{equation}
\mathbf{v}^2-\mathbf{v_1}^2=\mathbf{v_2}^2
\end{equation}
\begin{equation}
(\mathbf{v}+\mathbf{v_1})(\mathbf{v}-\mathbf{v_1})=\mathbf{v_2}^2
\end{equation}
\begin{equation}
\mathbf{v}+\mathbf{v_1}=\mathbf{v_2}
\end{equation}
\end{document}

好