Wandai Blog 共被围观 1,640,693 次

几何平均数

几何意义

　　我们知道算术平均数, (a+b)/2,体现纯粹数字上的关系, 而根号ab, 称为几何平均数, 这个体现了一个几何关系,

即过一个圆的直径上任意一点做垂线,

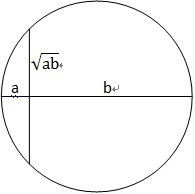
直径被分开的两部分为a, b

　　那么那个垂线在圆内的一半长度就是根号ab, 并且(a+b)/2>=根号ab

　　这就是它的几何意思, 也是称之为几何平均数的原因。

定义和公式

几何平均数(geometric mean)是n个变量值连乘积的n次方根。

根据资料的条件不同, 几何平均数有加权和不加权之分。

　　1、简单几何平均法

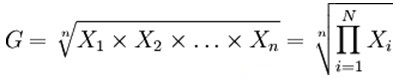
　　2、加权几何平均法

计算几何平均数应注意的问题

　　1、变量数列中任何一个变量值不能为0, 一个为0, 则几何平均数为0。

　　2、用环比指数计算的几何平均易受最初水平和最末水平的影响。

　　3、几何平均法主要用于动态平均数的计算。

几何平均数的特点

　　1、几何平均数受极端值的影响较算术平均数小。

　　2、如果变量值有负值, 计算出的几何平均数就会成为负数或虚数。

　　3、它仅适用于具有等比或近似等比关系的数据。

　　4、几何平均数的对数是各变量值对数的算术平均数。

主要用途

    几何平均数多用于计算平均比率和平均速度。如: 平均利率、平均发展速度、平均合格率等。

　　计算几何平均数要求各观察值之间存在连乘积关系, 它的主要用途是:

　　1、对比率、指数等进行平均

　　2、计算平均发展速度

　　其中: 样本数据非负, 主要用于对数正态分布。