今天, 是物理统练。
有一道看起来很简单的题目:
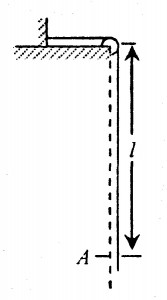
在一次消防演习中, 质量为 \(m=60kg\) 的消防员欲到达距离楼顶 \(l=40m\) 处的房间。如图所示, 他沿一条竖直悬垂的轻绳从静止开始匀加速下滑, 当他滑到该房间的窗户A处时, 突然停止下滑, 同时用脚踢开窗户, 自己反弹了一下, 然后进入窗内, 已知消防员从开始下滑到刚进入窗内共用了时间 \(t=10s\) , 试估算他沿绳子下滑时受到的摩擦力大小最接近
$$A.~100N~~~B.~300N~~~C.~550N~~~D.~900N$$
诶呀, 太简单了, 不就是牛二嘛!
由 \(\frac{1}{2}at^2=l\) 得 \(a=\frac{2l}{t^2}=0.8m/s^2\)。
再根据牛顿第二定律, \(mg-f=ma\) 得 \(f=552N\) ! 选 \(C\) !!!
然而, 事情没有想象的那么简单, 我们需要再次认真地读一下题目。
在一次消防演习中, 质量为 \(m=60kg\) 的消防员欲到达距离楼顶 \(l=40m\) 处的房间。如图所示, 他沿一条竖直悬垂的轻绳从静止开始匀加速下滑, 当他滑到该房间的窗户A处时, 突然停止下滑, 同时用脚踢开窗户, 自己反弹了一下, 然后进入窗内, 已知消防员从开始下滑到刚进入窗内共用了时间 \(t=10s\) , 试估算他沿绳子下滑时受到的摩擦力大小
发现不对, 好像还有一段运动是”反弹了一下, 然后进入窗内”, 那就是一段单摆运动。
那么这段单摆运动的时间是多长呢?
经过分析得到, 这是做了半个周期的单摆运动。
根据 \(T=2\pi\sqrt{\frac{l}{g}}\) 估算出周期约为 \(T=2*3*\sqrt{\frac{40}{10}}=12s\)
所以, \(t_2=\frac{1}{2}T=6s\), 于是 \(t_1=t-t_2=4s\)
然后再由 \(\frac{1}{2}a{t_1}^2=l\) 得 \(a=\frac{2l}{{t_1}^2}=5m/s^2\)。
再根据牛顿第二定律, \(mg-f=ma\) 得 \(f=300N\) 。 选 \(B\) 。
太遗憾了。
六分呐。
再次反思一下, 为什么当时没有想到这一点。可能还是没有认真读题, 仔细分析运动过程。
其实, 当时做完这道题目的时候, 我还想了一下, 怎么这么简单, 不像现在应该做的题。结果, 它果然有坑。

所以仔细审题非常非常重要啊
坑题害死人啊!